Михаил  Щеглов,

кандидат технических наук, доцент КНИТУ-КАИ

 

 

МАТЕМАТИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ЧУДА?

 

Инженер по авиационным приборам из Казани Михаил Щеглов зафиксировал обрыв темпов роста заболеваемости коронавирусом в России, составив математическую модель динамики её развития

 

Если набрать в Яндексе слово «коронавирус», то выйдет информация, включающая графики роста заболеваемости за период с 30 марта по текущий день. Опубликованы и более детальные данные, например, на сайте коронавируса начиная с 3 марта. Поскольку уже скоро два месяца, как мы вплотную прикоснулись к данной теме, а неделю назад 20 апреля президент нашей страны сказал во всеуслышание что России удалось замедлить распространение коронавируса, то актуально провести анализ динамики развития процесса, чем я и занялся накануне. Как инженер, представитель точных наук.

Если смотреть на накопительный результат – общее число заболевших – график на рисунке справа, то он выглядит монотонным, гладким. Но если перевести взгляд на график, который слева, отображающий изменения числа вновь выявленных заболевших по дням, то первое же, что бросится в глаза всякому искушённому в вычислениях и визуализации их результатов, это то, что начальный этап вплоть до 19 апреля имеет ярко выраженный экспоненциальный характер. Этот рубеж на графике мною отмечен белой галочкой. Но далее, начиная с того самого понедельника 20 апреля и уже в течение недели «системности» в поведении графика не наблюдается, в первом приближении заболеваемость выглядит как постоянная средняя.

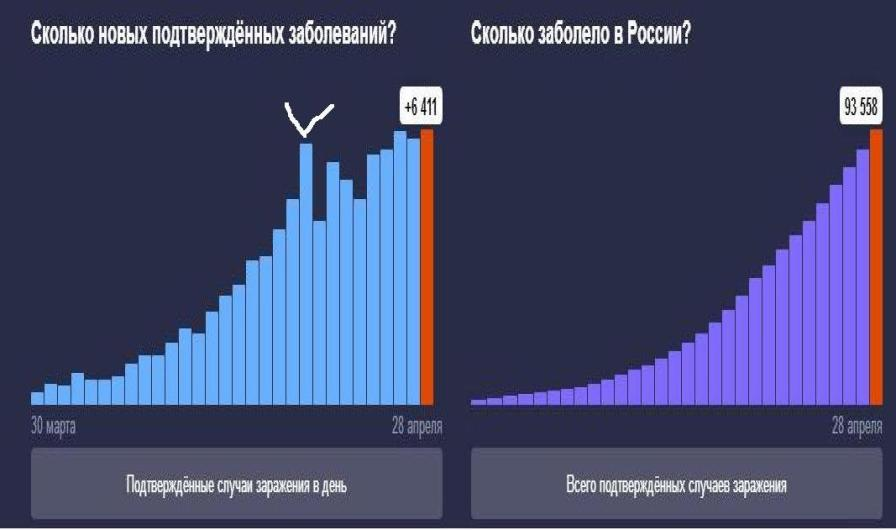
Графики развития пандемии коронавируса в России за период с 30 марта по 28 апреля 2020 г. по официальным данным Роспотребнадзора

Гипотезу свою я проверил собственноручно выполненным математическим расчетом.

Для определения математического выражения закона изменения числа вновь выявленных заболевших пользовался хорошо известным так называемым «методом наименьших квадратов», заложив данные со дня устойчивого характера роста вновь заболевших, с 18 марта. Проверил несколько видов зависимостей, оказалось, действительно, экспонента отображает закономерность с наибольшей точностью. Вот эта зависимость числа новых заболевших: y как математическая функция по дням от начала отсчёта x:

y=e ^{3.659+0.162 x}

Средняя погрешность этой зависимости по отношению к фактическим данным составляет не более 19.2%, что весьма неплохо для модели подобного рода явлений, да и, как я понимаю, согласуется с известными результатами исследования развития заразных заболеваний.

Результаты иллюстрирует рисунок, на нём голубыми плюсиками отмечены фактические значения, а красная линия – график полученной экспоненты. Чёрная горизонтальная линия – средний, начиная с 20 апреля, показатель 5677 вновь заболевших за сутки. Пока до сего дня 28 апреля этот показатель выполняется со средней погрешностью не более 9,8%

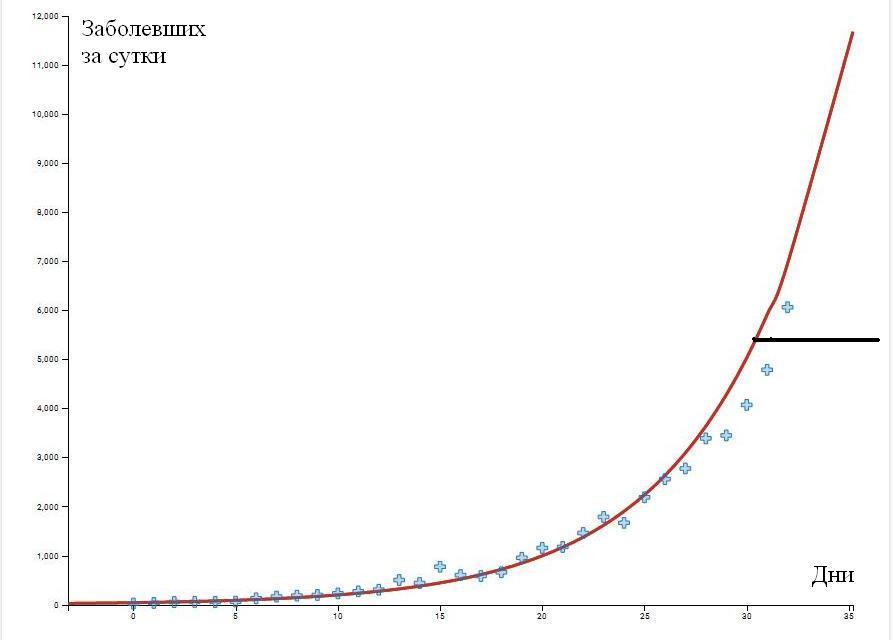
Графики вновь заболевших за сутки по России по дням, начиная с 18 марта.

Отмечу, что если бы выведенная экспонента продолжала бы действовать и после 19 апреля, то уже к 22 апреля новых заболевших было бы в течение суток вдвое больше, чем это среднее, а сегодня 28 апреля за сутки заболели бы не 6411 человек, как говорят фактические данные, а 24810. А сумма заболевших в России за период с того самого рубежного дня 19 апреля составила бы не 50705, как произошло фактически, а как показывают расчёты по полученной зависимости, 111321 человека, то есть численность больных практически бы удвоилась. А если точно , то за весь период заболевших было бы не 93558 человек, как сейчас на первом графике, который справа, а 154174!

Мои легендарные учителя по авиационному приборостроению учили меня, что в нашем деле главными являются две вещи: надёжность и точность.

Готов предоставить все расчёты интересующимся.

Но каким образом на последнем рисунке явно наметившаяся красным экспонента претерпела излом, превратившийся в горизонтальную чёрную линию, у меня, как представителя точных наук, ответа нет. Остаётся одно: считать, что в России на день Пасхи 19 апреля 2020 г. произошло чудо.